احتمال یا پیشآمد

احتمال یا پیشآمد

تاریخچه احتمال

پیدایش رسمی احتمال از قرن هفدهم به عنوان متدی برای محاسبه شانس در بازیهای قمار بوده است. اگر چه ایده های احتمال شانس و تصادفی بودن از تاریخ باستان در رابطه با افسونگری و بخت آزمایی و بازیهای شانسی و حتی در تقسیم کار بین راهبان در مراسم مذهبی وجود داشته است و به علاوه شواهدی از بکارگیری این ایده ها در مسایل حقوق٫ بیمه٫ پزشکی و نجوم نیز یافت میشود٫ اما بسیار عجیب است که حتی یونانیان اثری از خود در رابطه با استفاده از تقارنی که در هندسه بکار می برده اند در زمینه احتمال یا اصولی که حاکم بر مسایل شانس باشد بجا نگذاشته اند.
ارسطو پیشامدها را به سه دسته تقسیم می نمود:
۱) پیشامدهای قطعی که لزومآ اتفاق می افتادند.
۲) پیشامدهای احتمالی که در بیشتر موارد اتفاق می افتادند.
۳) پیشامدهای غیر قابل پیش بینی و غیر قابل شناسایی که فقط با شانس محض رخ میدهند.اما ارسطو به تعبیرهای مختلف احتمال اعتقاد نداشته و فقط احتمال شخصی که مربوط به درجه اعتقاد افراد نسبت به وقوع پیشامدهاست را معتبر می دانسته است.
پاسکال و فرما اولی کسانی هستند که در اوایل قرن هفدهم مسایل مربوط به بازیهای شانسی را مورد مطالعه قرار دادند و این دو نفر به عنوان بنیانگزاران تیوری ریاضی احتمال لقب گرفته اند. دانشمندانی از قبیل هی گنز کارهای آنها را ادامه داده و ویت و هلی این مسایل را در آمارهای اجتماعی بکار گرفتند. این علم جدید نخستین نقطه اوج خود را در اثر مشهوری از ژاکوب برنولی بدست آورد. در این اثر علاوه بر تعریف کلاسیک احتمال ریاضی٫ اساس خاصی از قانون اعداد بزرگ و کاربردهای احتمال در آمارهای اجتماعی نیز مطرح شده است.
در قرن هجدهم متفکران بزرگی چون دی مور٫ دانیل برنولی٫ آلمبرت٫ اویلر٫ لاگرانژ٫ بیز٫ لاپلاس و گاوس قسمتی از وقت خود را به این علم جدید اختصاص دادند. بیز در سال ۱۷۶۳ قانون معروف بیز را ارایه می دهد و لاپلاس در نوشته ای تمام موضوع علم احتمال را جمع آوری می کند. مهمترین قضایای حدی که در محاسبات احتمالی بکار می رفته و تاثیر احتمال در ریاضی٫ فیزیک٫ علوم طبیعی٫ آمار٫ فلسفه و جامعه شناسی در این اثر جمع آوری شده است
با مرگ لاپلاس در سال ۱۸۷۲ اوج پیشرفت این علم به اتمام رسید و علی رغم برخی تلاشهای فردی که ماحصل آنها کشف قضایایی چون قضیه اعداد بزرگ پواسون و یا نظریه خطاهای گاوس بود٫ بطور کلی احتمال کلاسیک ارتباط خود را با مسایل تجربی و علمی از دست میدهد. اما جریانهای متقابل ظاهر می شوند. به موازات پیشرفت نظریه ریاضی یک نظریه آمار به عنوان کاربردهایی از احتمال بوجود می آید. این نظریه در رابطه با مسایل مهم اجتماعی از قبیل اداره داده های آماری٫ مطالعه جمعیت و مسایل بیمه بکار می رفته است. اساس کار توسط افرادی چون کوتلت و لکسیز ریخته شده و توسط دانشمندانی چون فشنر(روانشناس)٫ تیله و برانز(منجمان)٫ گالتون و پیرسون(زیست شناسان) پیشرفت نموده است. این کارها در اواخر قرن نوزدهم در جریان بوده و در انگلستان و برخی دیگر از کشورها حرفه حسابگری٫ به مفهوم آماردانی که از اقتصاد و ریاضی هم اطلاعاتی دارد و در جمعیت شناسی و بیمه خبره می شود٫ رونق می یابد. از طرف دیگر فرمولهای کلاسیک ایده های احتمال میز مسیر پیشرفت و کاربردی خود را ادامه میدادند. در این قرن در تلاش برای روشن سازی پایه منطقی کاربردهای احتمال٫ وان میزز یک فرمولبندی جدید برای محاسبات احتمالی ارایه میدهد که نه تنها از نظر منطقی سازگار بوده بلکه نظریه ریاضی و تجربی پدیده های آماری در علوم فیزیکی و اجتماعی را پایه گذاری می نماید.
مدل کلاسیک احتمال توسط برنولی و لاپلاس معرفی شد. این مدل به دلیل فرض همطرازی و عدم امکان تکرار در شرایط یکسان و دلایل دیگر با اشکالاتی روبروست که بسیاری از پدیده های طبیعی بر آن منطبق نیستایده های اساسی نظریه تجربی احتمال که قرار دادن فراوانی نسبی بجای احتمال است در سال ۱۸۷۳ توسط پواسون ارایه گردید.
بسیاری از مسایل احتمال حتی قبل از بیان اصول آن توسط کلموگرف در سال ٫۱۹۳۳ با ابزارهای تجربی و حتی نظری توسط دانشمندان مطرح شده است. ولی کلموگرف با بیان اصول احتمال پایه این علم و ارتباط دقیق آنرا با مباحث ریاضی مستحکم می نماید.
در این زمان احتمال به عنوان یکی از شاخه های ریاضی٫ نه تنها کلیه ابزارهای ریاضی را جهت پیشرفت خود بکار می گیرد٫ بلکه توانسته کاربردهایی را در حل برخی از مسایل ریاضی داشته باشد. نظریه احتمالی اعداد٫ نظریه احتمالی ترکیبیاتی و کاربردهای شاخص احتمال در برخی از مسایل آنالیز٫ بعضی از کاربردهای احتمال در ریاضی هستند.
از طرف دیگر احتمال به عنوان زیربنای ساختاری و اصول ریاضی علم آمار٫ در جهت پیشرفت این علم و قوام بخشی به دستورات آن نقشی اساسی دارد.
مسایل جالب احتمال هندسی و نظریه احتمالی اعداد٫ شمه ای از زیبایی های احتمال است که همه اینها با هم زیبایی٫ کارآیی و توان علم احتمال را نشان میدهند. دهند...مفهوم احتمال در مورد ارتباط یا پیوند دو متغیر به کار می‌رود، به این معنی که ارتباط یا پیوند آنها به صورتی است که حضور، شکل، وسعت و اهمیت هر یک وابسته به حضور، شکل، و اهمیت دیگری است. این مفهوم به صورت محدودتر و در مورد ارتباط دو متغیر کمّی نیز به کار برده می‌شود^[۲].ریاضی‌دانان عددی بین صفر و یک را به عنوان احتمال یک رویداد تصادفی به آن نسبت می‌دهند. رویدادی که حتما رخ دهد، احتمالش یک است و رویدادی که اصلاً ممکن نیست رخ دهد احتمالش صفر است^[۳]. احتمال شیر آوردن در پرتاب یک سکه سالم است، همانطور که احتمال خط آوردن هم است. احتمال این‌که پس از انداختن یک تاس سالم شش بیاوریم است.به زبان سادهٔ‌ ریاضی احتمال، نسبت تعداد اعضای مجموعهٔ پیشامدهای دلخواه به تعداد اعضای مجموعهٔ تمام پیشامدهای ممکن است. مثلاً در مورد تاس، برای محاسبهٔ‌ احتمال آوردن عددی زوج، مجموعهٔ پیشامدهای ممکن هست: {۱٫۲٫۳٫۴٫۵٫۶} و مجموعهٔ پیشامدهای دلخواه هست: {۲٫۴٫۶}. تعداد اعضای مجموعهٔ دلخواه هست ۳ و تعداد اعضای مجموعهٔ پیشامدهای ممکن هست ۶. پس احتمال هست: جمع احتمال رخ دادن یک رویداد با احتمال رخ دادن رویداد مکمل آن، عدد یک می‌شود. مثلاً در تاس ریختن جمع "احتمال آوردن شش" (که است) با "احتمال نیاوردن شش" (که است) می‌شود یک.

معرفي بزرگان احتمالات

چبیشف در ۱۶ ماه مه ۱۸۲۱ در "اکتاوو"٬ روستایی کوچک در روسیه غربی٬ در غرب مسکو متولد شد.هنگام تولد او پدرش از ارتش بازنشسته شده بود٬ اما اخیرآ در زندگی نظامی اش بعنوان افسر مقابل نیروهای متجاوز ناپلئون جنگیده بود. چبیشف در خانواده ای کوچک که جزئی از خانواده ای بزرگ با تاریخچه ای جالب توجه به دنیا آمد.والدین اش ۹ فرزند داشتند که برخی از آنها شغل پدرشان را پیش گرفتند.
تحصیلات ابتدایی او در خانه شکل گرفت . وی در منزل توانایی های اولیه خواندن٬ زبان فرانسه و حساب را یاد گرفت.بعدها زبان فرانسه برای او بسیار سودمند بود چون توانست با تکیه بر آن فرانسه را از نزدیک ببیند و ریاضیات پیچیده را به فرانسوی در همانجا بخواند. همین طور زبان فرانسوی بین ریاضیدانان پیشرو اروپایی زبان ارتباطی مؤثری بود.
در سال ۱۸۳۲ وقتی یازده ساله بود٬ خانواده اش به مسکو رفتند.در آنجا او درس خواندن را در خانه ادامه داد ولی در آن زمان توسط پی.ان.پاگورلسکی- کسی که به بهترین مدارس ابتدایی آموزش ریاضیات در مسکو رسیدگی می کرد- در ریاضیات آموزش داده می شد. پاگورلسکی نویسنده بعضی از مشهورترین کتب درسی ریاضی مدارس ابتدایی در آن زمان و به طور قطع ریاضیات را به دانش آموزان القا می کرد و به آنها آموزش قوی ای از ریاضیات می داد.بنابراین٬ چبیشف خیلی خوب برای درس خواندن در علوم ریاضیات آماده شد وقتی که در سال ۱۸۳۷ به دانشگاه مسکو- این دانشگاه در سال ۱۷۵۵تأسیس شد- رفت.
در دانشگاه مسکو کسی که تأثیر زیادی بر چبیشف گذاشت "نیکولای مترویوچ برشمن"- پروفسور ریاضیات کاربردی در دانشگاه مسکو از سال ۱۸۳۴- بود. چبیشف همیشه به تأثیر بزرگ برشمن بر خود هنگام تحصیل در دانشگاه اعتراف می کرد و او را مهمترین عامل در رسیدن به نتایج تحقیقاتش عنوان می کرد.
دپارتمان فیزیک و ریاضی در دانشگاه او در سال تحصیلی ۴۱-۱۸۴۰ یک مسابقه برگزار کرد و چبیشف در مقاله ای (y=f(x را با استفاده از بسط سری ها برای توابع معکوس پذیر حل کرد ولی مقاله او در آن زمان تنها جایزه دوم را به خود اختصاص داد و در سال ۱۹۵۰ منتشر شد. چبیشف در سال ۱۸۴۱ فارغ التحصیل شد و تحصیلات خود را در فوق لیسانس تحت حمایت استاد محبوبش "برشمن" ادامه داد.
اولین مقاله او به زبان فرانسه٬در رابطه با انتگرالهای چندگانه ٬در سال۱۸۴۳ درمجله "liouvill" منتشر شد. دومین مقاله او نیز به زبان فرانسه بود و این بار در سال ۱۸۴۴ در مجله "crelle" به چاپ رسید. این مقاله در رابطه با همگرایی سری تیلور بود.
در تابستان ۱۸۴۶ چبیشف در حال رسیدگی به رساله دکترای خود بود و در همان سال مقاله ای در مجله crelle بر پایه رساله خود منتشر کرد. رساله او در زمینه تئوری احتمال بود و در آن نتایج حاصل از تئوری احتمال را توسعه داد ولی با روشی ابتدایی.ناگفته نماند که رساله چبیشف تا پس از مرگ او به چاپ نرسید ولی او مقاله ای در رابطه با نتایج آن را در سال ۱۸۵۳ به چاپ رساند.
او همچنین در زمینه تئوری اعداد نیز مقالاتی به چاپ رسانده است.از جمله کارهای ناتمام او نزدیک شدن به اثبات قضیه اعداد اول است.اثبات اینکه اگر (p(n تعداد اعداد اول کوچکتر یا مساوی n باشد در این صورت حد p(n)logn/n وقتی n به سمت بی نهایت میل می کند برابر ۱ خواهد بود.او نمی توانست ثابت کند که این حد برابر یک است در حالیکه این حد وجود دارد. اثبات این قضیه ۲ سال بعد از مرگ او مستقلآ توسط "هدمرد" و "de la Vallee" ارائه شد.
همان طور که قبلآگفته شد چبیشف تئوری احتمال را بیان کرد. در سال ۱۸۶۷ او مقاله ای در رابطه با مقدار میانی را که در آن از نابرابری Bienayme استفاده شده بود چاپ کرد. یکی از نتایج این کار او نابرابری ایست که امروزه به آن نابرابری چبیشف-بینیم گفته می شود. ۲۰ سال بهد چبیشف دو قضیه در رابطه با اختمال را منتشر کرد٬ یکی اساس بکاربردن تئوری احتمال در داده های آماری و دیگری عمومی کردن قضیه حد مرکزی دوموآور-لاپلاس.
و اما زندگی خصوصی او٬ او هرگز ازدواج نکرد و تنها در یک خانه بزرگ با ده اتاق زندگی می کرد و از نظر مالی بی نیاز بود. و سر انجام در ۸ دسامبر ۱۸۹۴ در سنت پترزبورگ در روسیه درگذشت. مارکوف٬ فارغ التحصیل دانشگاه سنت پترزبورگ در سال ۱۸۷۸ بود. وی در سال ۱۸۸۶ مدرک پروفسوری خود را دریافت کرد. کارهای زودهنگام مارکوف در تئوری اعداد٬ آنالیز٬ حدود انتگرال ها٬ همگرایی سری ها٬ دنباله کسرها و ... بسیار اساسی بود.
بعد از سال ۱۹۰۰ ٬ مارکوف تحت تأثیر استاد خود چبیشف٬ از روش دنباله های کسرها در تئوری احتمالات استفاده کرد.وی هم چنین در مورد رشته های متغیرهای وابسته متقابل٬ مطالعاتی انجام داد.با این امید ثابت کردن قوانین حدی در احتمالات در حالات کلی آنها.او قضیه حد مرکزی را با در نظر گرفتن فرض های کامل آن٬ اثبات کرد.
مارکوف به دلیل مطالعاتش پیرامون زنجیرهای مارکوف که رشته هایی از متغیرهای تصادفی هستند٬ معروف است.در زنجیرهای مارکوف٬ متغیر بعدی توسط متغیر کنونی مشخص می شود ولی از راهی که تا کنون طی شده است مستقل است.
در سال ۱۹۲۳ "نوربرت واینر" اولین کسی بود که پیرامون یک سلسله از این مراحل مارکوف شروع به بحثی جدی کرد.اساس یک تئوری اصلی در سال ۱۹۳۰ توسط کولموگروف فراهم شد.
مارکوف به شاعری هم علاقه مند بود و پیرامون ساختار شعری مطالعاتی انجام داد.جالب اینکه کولموگروف هم٬ چنین علایقی داشت.مارکوف پسری به اسم خودش داشت که در ۹ سپتامبر ۱۹۰۳ به دنیا آمد و راه پدرش را ادامه داد.

مفهوم احتمال در مورد ارتباط یا پیوند دو متغیر به کار می‌رود، به این معنی که ارتباط یا پیوند آنها به صورتی است که حضور، شکل، وسعت و اهمیت هر یک وابسته به حضور، شکل، و اهمیت دیگری است. این مفهوم به صورت محدودتر و در مورد ارتباط دو متغیر کمّی نیز به‌کار برده می‌شود.

ریاضی‌دانان عددی بین صفر و یک را به عنوان احتمال یک رویداد تصادفی به آن نسبت می‌دهند. رویدادی که حتما رخ دهد، احتمالش یک است و رویدادی که اصلاً ممکن نیست رخ دهد احتمالش صفر است. احتمال شیر آوردن در پرتاب یک سکه سالم $\frac {1} {2}$ است، همانطور که احتمال خط آوردن هم $\frac {1} {2}$ است. احتمال این‌که پس از انداختن یک تاس سالم شش بیاوریم $\frac {1} {6}$ است.

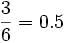
به زبان سادهٔ ریاضی احتمال، نسبت تعداد اعضای مجموعهٔ پیشامدهای دلخواه به تعداد اعضای مجموعهٔ تمام پیشامدهای ممکن است. مثلاً در مورد تاس، برای محاسبهٔ احتمال آوردن عددی زوج، مجموعهٔ پیشامدهای ممکن هست: {۱٫۲٫۳٫۴٫۵٫۶} و مجموعهٔ پیشامدهای دلخواه هست: {۲٫۴٫۶}. تعداد اعضای مجموعهٔ دلخواه هست ۳ و تعداد اعضای مجموعهٔ پیشامدهای ممکن هست ۶. پس احتمال هست: $\frac {3}{6}=0.5$

جمع احتمال رخ دادن یک رویداد با احتمال رخ دادن رویداد مکمل آن، عدد یک می‌شود. مثلاً در تاس ریختن جمع "احتمال آوردن شش" (که $\frac {1} {6}$ است) با "احتمال نیاوردن شش" (که $\frac {5} {6}$ است) می‌شود یک.